
Have you ever wanted to learn the basics of Roulette math in just a few minutes? No? Well, too bad, because I'm going to teach them to you anyway! The good news for you is that the basics are dead simple, and I promise it'll be painless.
Eyeballing Payouts
If you're starting your Roulette education from scratch, the first thing you'll need to learn is the payouts for the various bets. You can wager on 1 number up to as many as 18 numbers on a single bet and each wager pays out at different odds depending on your chances of winning.
Luckily, it's easy to figure out the payouts of each of these bets, and you don't need to memorize a big table or learn a complicated formula (although we will look at tables and formulas later on). For almost all of the bets, you can determine the payout by eyeballing the layout and slicing and dicing it visually.
The trick is knowing that there is NO house advantage (a.k.a "house edge") in Roulette if we
remove the zeroes
(



So to figure out how much each bet pays out, just keep making the same type of bet until you've covered all 36 numbers (ignoring the zeroes) and count the number of losing bets that would need to pay out your the winning bet.
Keep in mind that there's no reason to ever bet on all 36 numbers, since would be no chance of making money on the bets as a whole. We're just doing it here hypothetically for illustrative purposes.
1-Number Bet: "Straight-Up"
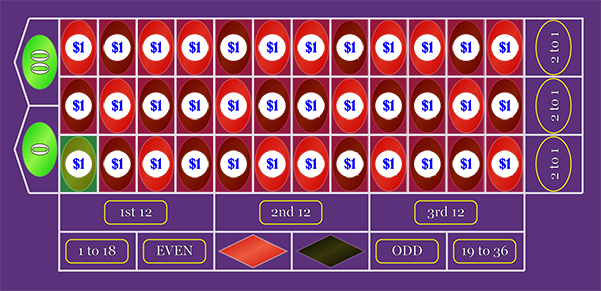
There are 36 non-zero numbers, so if you bet on all 36 "Straight-Up" bets, your spin will have one winner (if we assume it doesn't land on one of the zeroes) and 35 losers. So for the losses to pay off the winner, the Straight-Up bet needs to pay 35 to 1.
2-Number Bet: "Split"
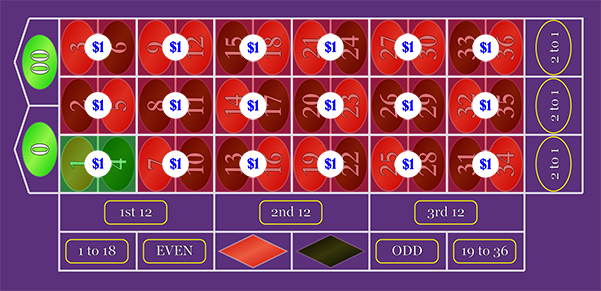
You can make 18 "Split" bets to cover up the entire non-zero field. For the Split bet scenario, you have to make sure there is no "overlap" in your bets, where hitting a single number would result in more than one Split bet winning.

 hits
hits
The 17 losing bets will pay off the winning bet, so the 2-number bet pays 17 to 1.
3-Number Bet: "Street"
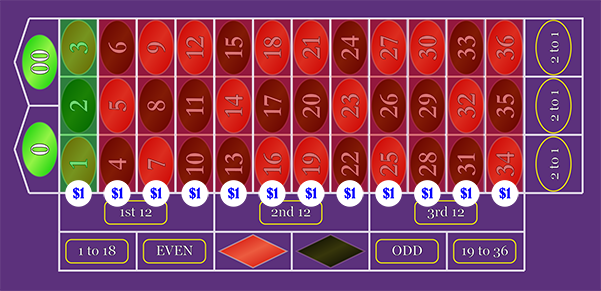
You can bet on all 12 "Streets" (each street is a row on the layout), and the 11 losing bets will pay off the one winner at a rate of 11 to 1.
4-Number Bet: "Corner"
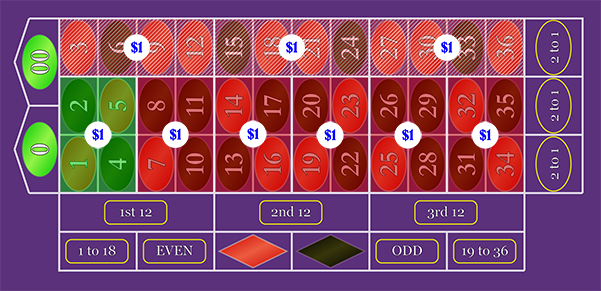
This one is a little tricky, because you kind of have to warp the definition of a "Corner" bet. A Corner bet is placed in the 4 corners where 4 numbers join, but since the layout has 3 columns, there will be a column that would remain uncovered.
There wouldn't be an issue with a casino allowing some type of "a-la-carte" 4-number bet where all four
numbers were in a straight line (for example, if you could make a 4-number bet on the




The important take away is that you can group the 36-number layout into 9 groups of 4. And winning with one of the groups, you would bet paid 8-to-1 from the 8 losing groups.
5-Number Bet: "Top-Line"

We're going to skip this bet for now. The five-number "Top-Line" bet is only possible by betting on





It's also the only bet that can't evenly split the 36 number field (since 36 is not evenly divisible by 5) and consequently, it's the only bet that doesn't offer fair odds when we assume a wheel with only 36 spots.
6-Number Bet: "Double-Street"
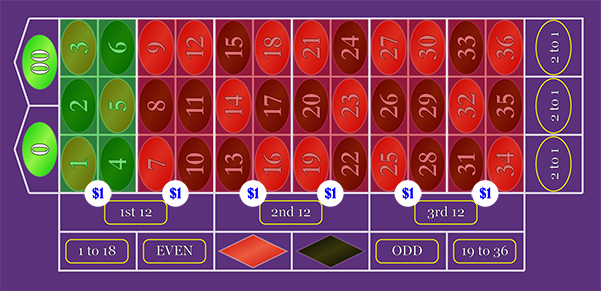
Pays 5 to 1. Hopefully, you've figured out how this works by now.
12-Number Bet: "Dozen" or "Column"
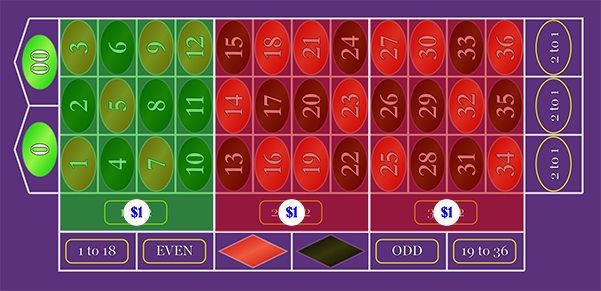
Pays 2 to 1.
18-Number Bet: "Red"/"Black", "Even"/"Odd", "1st Half"/"2nd Half"
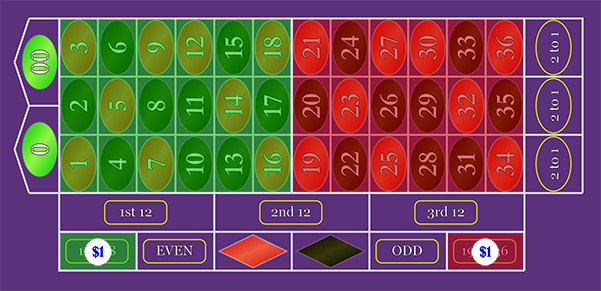
Pays 1 to 1 (even money).
The Payout Formula
If you're not a visual person like me and you don't want to visualize the Roulette betting layout every time you want to calculate the payouts, you can just use the following formula:
This should be easy to understand because it's the formulaic representation of the slicing and dicing we saw above.
We took the 36-number layout, divided it by the number of spots we want to bet on at a time (n) and then subtracted the 1 winning bet to see how many losing bets we need to pay off the winner.
For you non-visual learners, here's a table with all the calculations you need to determine the payouts:
| Bet | n | Payout |
|---|---|---|
| Straight Up | 1 number |
|
| Split | 2 numbers |
|
| Street | 3 numbers |
|
| Corner | 4 numbers |
|
| Top-Line Bet | 5 numbers | (does not conform to formula) |
| Double Street | 6 numbers |
|
| Dozen/Column | 12 numbers |
|
| Half | 18 numbers |
|
Calculating the House Advantage
Since we know that a zeroless Roulette wheel has no house advantage (for all bets besides the 5-number bet), we can simply calculate the house edge by calculating the probability of hitting any of the zeroes on the wheel.
| Wheel Type |
Probability of hitting any zero |
House Advantage % |
|---|---|---|
| Single Zero |
|
2.70% |
| Double Zero |
|
5.26% |
| Triple Zero |
|
7.69% |
That Pesky 5-Number "Top-Line" Bet
To calculate the house advantage of any bet, you can use the more generic formula:
Where n is the number of spots covered, p is the payout for the n-number bet, and z is the number of zeroes on the wheel.
For all the bets we've covered so far, the
But since the number 5 doesn't divide evenly into 36, it's not possible to have a fair payout that is a nice round number. That's why casinos short-change you on the payout of this bet by only paying you 6-to-1 instead of 6.2-to-1, making the 5-number bet the persona non grata of Roulette bets.
To calculate the house advantage of the Top-Line bet on the Double Zero wheel, we get
Here is the house edge on the 5-number bet for the various wheel configurations:
| Wheel Type | House Advantage of Top-Line Bet |
|---|---|
| Single Zero | Top-Line Bet not possible |
| Double Zero |
|
| Triple Zero |
|
The Top-Line bet is truly the WORST bet available on one of the worst table games. So, if you ever find yourself betting the Top-Line, you should ask yourself this question:

Comparing Roulette to Other Table Games
So, now you know the house advantage for Roulette. In the US (where Double Zero wheels are the norm), it's 5.26% per bet and that is HUGE.
The house edge for 6-deck Blackjack is only about 0.42% if you play perfect Basic Strategy, making Roulette 12 and a half times worse!
And here's how Roulette stacks up against the most popular casino table games.
| Table Game | House Advantage |
|---|---|
| 6-Deck Blackjack | 0.42% |
| Baccarat (Banker Bet) | 1.06% |
| Craps (Pass/Come) | 1.41% |
| Double Zero Roulette | 5.26% |
Roulette doesn't have as many events (i.e. spins) per hour as the other table games, but even with this factor working to the player's benefit, the hourly loss for the game is horrendous.
In Blackjack, betting $10/hand at 105 hands/hour (an estimate for a table with 3 players) with a house edge of 0.42%, your hourly loss is about
In Roulette, betting $10/spin at 60 spins/hour (again, estimating for a 3 player table) with a house edge of 5.26%, your hourly loss is about

You're Now a Roulette Math Expert!
Congratulations! You now know about 99% of what you need to know about Roulette Math!
There's really not a lot to this game and I think the people who enjoy it are drawn in by its simplicity. Of course, casinos recognize this and it is their reason for charging patrons with an EXORBITANT house advantage of 5.26%.
You're being penalized for not taking the time to learn Blackjack.
You're being penalized for not having enough money to play Baccarat.
You're being penalized for being intimidated by the Craps layout.
Now that you're an expert, hopefully you recognize that Roulette is one of the absolute WORST games out there. And if you're looking to interpret any of the numbers we've calculated above, you should follow what I call "Roulette Basic Strategy":
Avoid Roulette.
If you must play Roulette, find a Single Zero game.
If you can't find or afford a Single Zero game NEVER play a Triple Zero game.
And no matter what, NEVER play the 5-number Top-Line bet.
